
28. A gyorsítási munka, a mozgási és a rugalmas energia
28. A gyorsítási munka, a mozgási és a rugalmas energia
A gyorsítási munka
Egy m tömegű test nyugalomból indul vízszintes, súrlódásmentes síkon. A síkkal párhuzamos F erő hat rá, amely s úton munkát végez.
Az F=m*a erő munkája: Wgy=F⋅s
A test a gyorsulással mozog, v a sebessége az út végén:
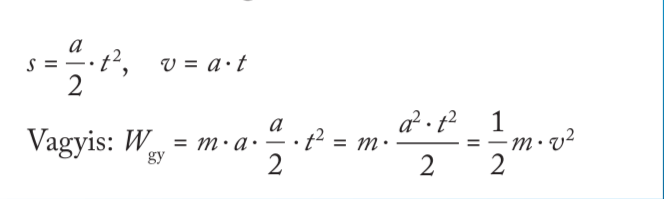
Kinematikai összefüggések alapján levezethető. TNK: 98. o.

👉 Következtetés: A gyorsítási munka egyenlő a test mozgási energiájának növekedésével.
A mozgási energia

Munkatétel

Rugalmas energia
A rugó megnyújtásakor vagy összenyomásakor munkát végzünk, amely a rugóban energiaként tárolódik. Ez az energia a rugó visszaállásakor mozgási energiává alakulhat (pl. kiskocsi gyorsítása).
A rugóban tárolt energia képlete:

D = rugóállandó (N/m),
Δl = megnyúlás vagy összenyomás.
Az energia a megnyúlás négyzetével arányos, ezért kétszeres nyújtás négyszeres energiát jelent.
A rugóerő munkája negatív, mert az erő az elmozdulással ellentétes irányú, de ennek –1-szerese adja a rugóban tárolt energiát.
Feladatok
Forrás:
https://aimunkafuzet.webnode.hu/27-a-munka-teljesitmeny/
6, 8, 15, 16, 19, 25, 26, 33, 43, 45, 58
6. Két azonos irányba haladó vasúti kocsi összeütközik,
összekapcsolódik, s együtt mozog tovább. Mit mondhatunk a két összekapcsolódott
kocsi együttes mozgási energiájáról?
Válasz: C Kisebb lesz, mint az ütközés előtti összeg.
Indoklás: Rugalmatlan ütközésnél a mozgási energia egy része hővé és deformációs energiává alakul.
8. Egy rugót 20 cm-rel megnyújtunk kétféle módon: Az egyik végét a falhoz rögzítjük, a másikat húzzuk ki. Az egyik végét megfogjuk, a másikat a másik kezünkkel húzzuk ki 20 cm-rel. Melyik esetben végzünk kevesebb munkát?
Válasz: C – Egyenlő munkát végzünk mindkét esetben.
Indoklás: A rugó energiája csak a megnyújtás mértékétől függ, nem a módszertől.
8. Egy rugót 20 cm-rel megnyújtunk kétféle módon: Az egyik végét a falhoz rögzítjük, a másikat húzzuk ki. Az egyik végét megfogjuk, a másikat a másik kezünkkel húzzuk ki 20 cm-rel. Melyik esetben végzünk kevesebb munkát?
15. Rugó megnyújtása 5 cm-ről 10 cm-re. Mennyi energia
kell?
Válasz: C – Több mint 20 J.
Indoklás: A rugó energiája a megnyújtás négyzetével arányos, így a második szakaszhoz több energia kell.
16. Függőlegesen feldobott test mozgási energiája a kezdeti
érték felére csökken. Mekkora úton?
Válasz: B – h/2.
Indoklás: A mozgási energia lineárisan csökken a magassággal, feleződéskor a test fél magasságig jut.
19. Két test közül az egyiknek nagyobb a lendülete. Mit
mondhatunk a mozgási energiájukról?
Válasz: B – Nem állapítható meg.
Indoklás: A lendület I = m·v, az energia E = ½ m·v²; a tömeg és sebesség aránya nem ismert.
26. Rugós puska 5 cm összenyomás → 3 m magasra lő. 10 cm összenyomásnál?
Válasz: C – 12 m magasra.
Indoklás:
A rugó energiája a
megnyomás négyzetével arányos, kétszeres összenyomás négyszeres energiát ad.
33. Artisták kilövése rugóval, Géza 80 kg, János 60 kg.
Melyik repül magasabbra?
Válasz: C – Géza kb. háromnegyed olyan magasra repül, mint János.
Indoklás: Azonos rugóenergia oszlik meg, nagyobb tömeg → kisebb emelkedési magasság.
43. Mikor végzünk több munkát? 2 kg test 4 m/s-ra vagy 4 kg test 2 m/s-ra?
Válasz: A – Ha 2 kg-os testet 4 m/s-ra gyorsítunk.
Indoklás: E = ½ m·v² → ½·2·16 = 16 J, míg a másik esetben ½·4·4 = 8 J.
45. Lövedék fékútja kétszeres sebességnél. Hogyan változik?
Válasz: C – Több mint kétszeresére nő. (Négyszeresére.)
Indoklás: A fékút arányos a sebesség négyzetével, így kétszeres sebességnél négyszeres fékút.
58. Kamion (20 t, 80 km/h) vs. sportkocsi (1,5 t, 320
km/h). Melyiknek nagyobb a mozgási energiája?
Válasz: B – A sportkocsinak.
Indoklás: A mozgási energia ½ m·v², a nagy sebesség sokkal jobban növeli az energiát, mint a tömeg.
25. Autó gyorsulása 30 km/h-ról 90 km/h-ra. Hogyan változik
a mozgási energia?
Válasz: C – Kilencszeresére nő.
Indoklás: A mozgási energia a sebesség négyzetével arányos, (90/30)² = 9.
